Sleeping Beauty and the Forever Muffin
Most philosophical puzzles don’t have clean answers, but this one does
Today, I’m going to be writing about the Sleeping Beauty (SB) problem, a famous question in the field of philosophy. For those of you who don’t know what the SB problem is or why it’s so important our understanding of our own existence, I’ll explain it in detail in the first section. For the rest, you can skip past that and dive into the discussion.
There has been a huge amount said about the SB problem over the years. But at the end of the day, it’s really just a math problem, and though it’s tricky the math itself is not actually all that complicated, making pretty accessible. I’ve read more about it than I care to admit and certainly more than I ever intended to, and at the end of the day I’ve noticed that everyone seems to be making one of a few distinct arguments - most of which are either outright wrong or miss the point. In particular, many people make arguments that seem to be addressing subtlety different questions, yielding answers that simply do not apply in the context of the original problem.
So what I’m going to do is break down all of these different “interpretations.” I’m going to go one by one, explaining why each is wrong, and I’m go to do my best to really target the exact point in the argument where the reasoning breaks down.
Importantly, once I’ve explained each interpretation, I’m going to tie each one back into the “universe question,” asking how each model would apply if we used the same reasoning to explain our universe. When playing with these kinds of toy problems, it can be easy to lose sight of the original context - but real insight necessitates that we don’t let that happen.
Unfortunately, this will require a few equations, though it will be nothing beyond very basic probability (P(X) is “probability of X,” P(X|Y) is “probability of X once we know Y is definitely true,” etc). I’m including it mostly to show that I’m not making all this up, and because there’s a lot of subtlety in how this problem can be presented.
But I also want my writing to be broadly accessible, so I took care that those who are not interested in the math should be able to just take my word for it, letting their eyes glaze over the equations and have no problem understanding the points being made.
The Sleeping Beauty Problem and Fine-Tuning
(If you know all about the Sleeping Beauty Problem and how it ties into fine-tuning and anthropics, you can skip this.)
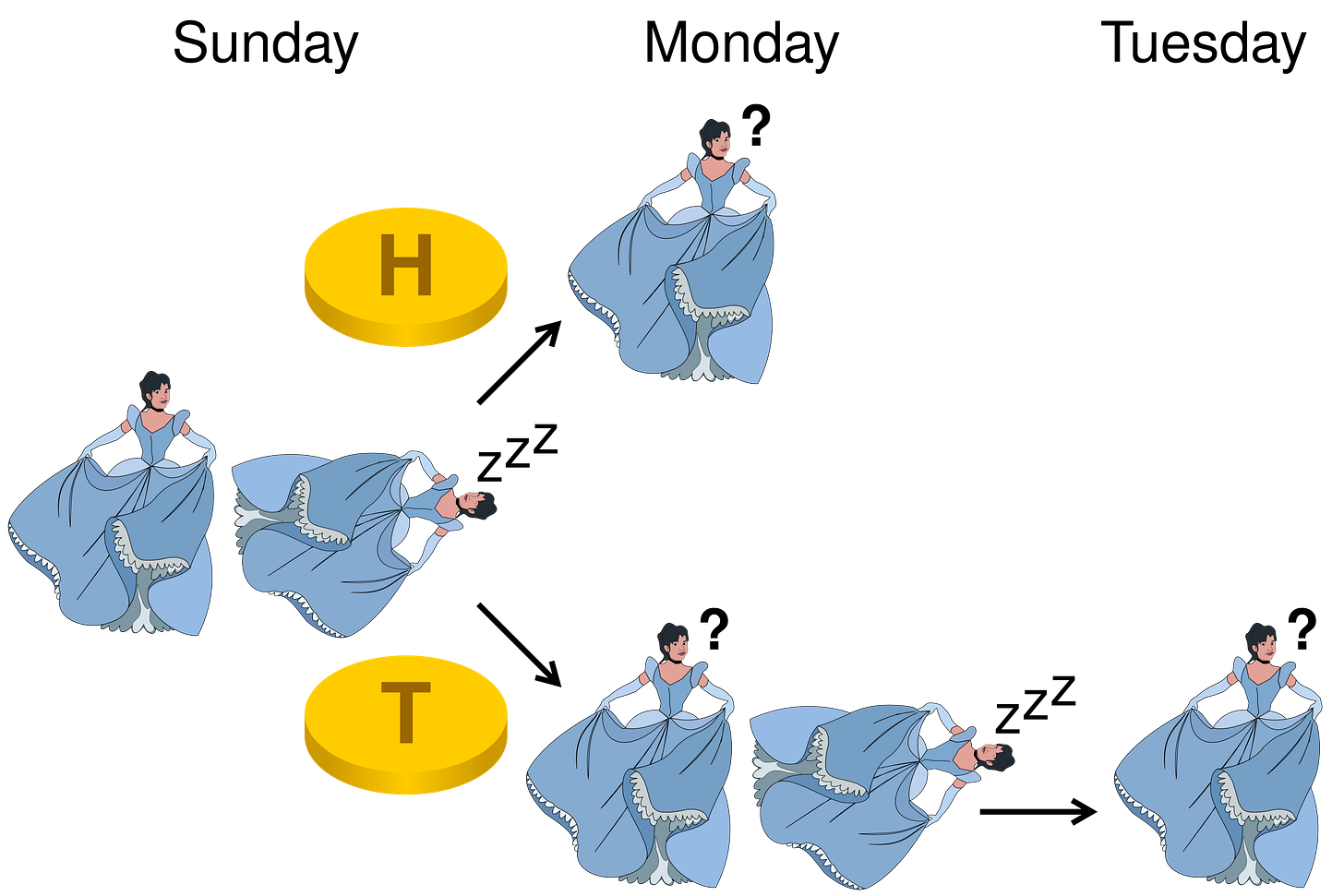
Lately, I’ve been thinking a lot about the Sleeping Beauty Problem. For those who don’t know, it’s an old philosophical puzzle that goes like this:
Some scientists put Sleeping Beauty to sleep.
They flip a coin.
If the coin comes up heads, they will wake sleeping beauty up exactly once and ask her to guess the result of the flip.
If the coin comes up tails, then they will wake her up twice and ask her twice to guess the result of the flip, wiping her memory in between. The wiping of her memory is essential: each wake up is completely independent.
And the question is “when she wakes up, what odds should Sleeping Beauty give that coin came up heads?”
Right off the bat, there’s an issue: “should” is actually not well-defined in this context. There are a few slightly different but superficially similar questions you can ask, and depending on how you phrase Sleeping Beauty’s goal, the odds of “heads” may seem to be either one third (since 2/3 of wake ups happen on tails) or one half (since there’s a 50% chance a coin comes up heads).
In isolation, this is fine - “it depends” is a perfectly valid answer when there isn’t any reason to favor one approach over another. In practice, though, this problem isn’t being presented in isolation.
Rather, it’s usually presented in the context of the “fine-tuning” problem - the philosophical question of why all the constants of our universe (the force of gravity, the nuclear forces holding atoms together, etc.) all seem so fine-tuned for life, when the slightest deviation would not just prevent life but make matter as we know it impossible.
There are two main ways this question typically gets answered. The first is that the universe was created by God or some other deity, while the second is an appeal to something called the Anthropic Principle - the claim that of course the universe is fine-tuned, we wouldn’t be here if it wasn’t. It gives us a reason not to be surprised by the universe’s parameters - there could be any number of other universes, but we wouldn’t know about them because we weren’t there. It tells us very little about the universe, but at least it’s strong enough to give us an alternative explanation beyond “God did it.”
Enter the Sleeping Beauty problem. In both problems - SB and what I will call the “universe” or “fine-tuning” problem, we’re trying to decide which possible cause is most likely for the universe we’re in. The two options in SB - heads or tails - correspond to the different origins our universe may have, and SB’s 50-50 odds correlate with the different priors we might give to each origin we consider1
And for that reason, the answer you give to the SB problem also has implications for how we ought to understand our universe. Whereas the 1/2 position would bring us back to the Anthropic Principle - giving no preference for any particular explanation - the 1/3 position would imply that, all else being equal, we ought to believe in whichever explanation creates the most people. The writer Bentham’s Bulldog, for instance, has staunchly defended this approach, arguing from the “thirder” position that we ought to assume the universe is infinite, and only God could produce infinite people.
The Halfer Position
Remember always that the point of all of this is to help us understand how we ought to model our own universe; we want to be solving the version of the problem that’s most relevant to that question. Part of doing that means asking exactly the correct question.
In this case, the correct question is this: “Now that we’re awake, what are the odds the coin came up heads?” In math, I will write this as P(Heads | Awake), or simply P(H | A) (In addition to “A” and “H” for “awake” and “heads”, I will also use the letter “T” for “tails”.) In terms of the universe question, this is the equivalent of asking “based on what we know and observe, which explanation for the universe is most likely?”
I suspect the intuitive position in SB for most people is probably 1/3 (that is, P(H|A) = 1/3). I admit that that was what jumped into my head the first time I heard it, before doing any math. However, if you actually do the math in the most “naive” way (that is, if you just write it out and try to solve it), you’ll seem to get 1/2 (using Bayes Rule and the fact that you wake up at least once in each scenario, meaning P(A) = P(A|H) = 1):
This result seems counter-intuitive, but as I’ll discuss it’s actually quite correct. The simplest way I can think to explain it is that the answer is 1/2 because which universe we are in was actually determined by the coin when it flipped, whereas the wake ups only came afterwards when the truth was already fixed. There’s also a bit of a Monty-Hall-like effect here, where certain values unexpectedly change - it turns out everything balances because you’re actually twice as likely to be a Sleeping Beauty who wakes up on heads as opposed to tails.
Still, if neither of those explanations are convincing to you, hang tight - I’m going to explain it more as we go.
Thirder Interpretation 1: The Warehouse of Souls
Let’s give these positions a better name than just “halfer” and “thirder.” The term of art for the thirder position - coined by Nick Bostrom - is the “Self-Indication Assumption” or “SIA.” The official definition is that one should reason as if they were selected from all possible observers. In practice, what that really means is that we ought to “weight” our guesses by the number of possible people in the universe we’re trying to predict. There are 3 “possible” people in the Sleeping Beauty problem, therefore by the SIA we ought to give ourselves 1-in-3 odds of heads.
The opposite assumption is the “Self-Sampling Assumption” or “SSA.” Which for our intents and purposes basically just means that we shouldn’t weight our guesses by the number of possible people - 50% chance of coin coming up heads means SB must guess 50%.
I already gave the math of the SSA, but as I alluded to there are actually several ways to “interpret” the SIA into actual math.
For the first of these interpretations, I’m going to change up the Sleeping Beauty problem just a tiny little bit and add another narcoleptic princess - let’s call her “Snow White.” When the coin comes up heads, we only wake Sleeping Beauty. When the coin comes up tails, we wake up both Sleeping Beauty and Snow White. Importantly, both Snow White and Sleeping Beauty have had pieces of their memories wiped, so neither remembers which they are when they wake up. The math doesn’t really change, but now everything’s a little easier to talk about.
What we need to figure out is how to make the odds of heads after waking into 1/3. One way is to claim that we’re twice as likely to wake up on tails as heads: P(A | T) = 2 * P(A | H). This does what we need, and we wind up with 1/3 odds of heads on waking:
Easy enough, and on first glance, it seems we’re done; as far as I know this interpretation is the standard one for the SIA. It almost works out, except that there’s a weird twist: you wind up also with a significant chance of not waking up at all.
To see what I mean, let’s take a look closer at how we formalized “twice as likely to wake on tails.” We said P(A | T) = 2 * P(A | H), but we never gave either value a real number. So let’s make some numbers up and say P(A | T) = 1 and P(A | H) = 1/2. But if P(A | H) = 1/2, that means that P(not A | H) must also be 1/2, since P(A | H) + P(not A | H) must equal 1.
But what does that actually mean? Clearly, someone always wakes up whether the coin comes up heads or tails.
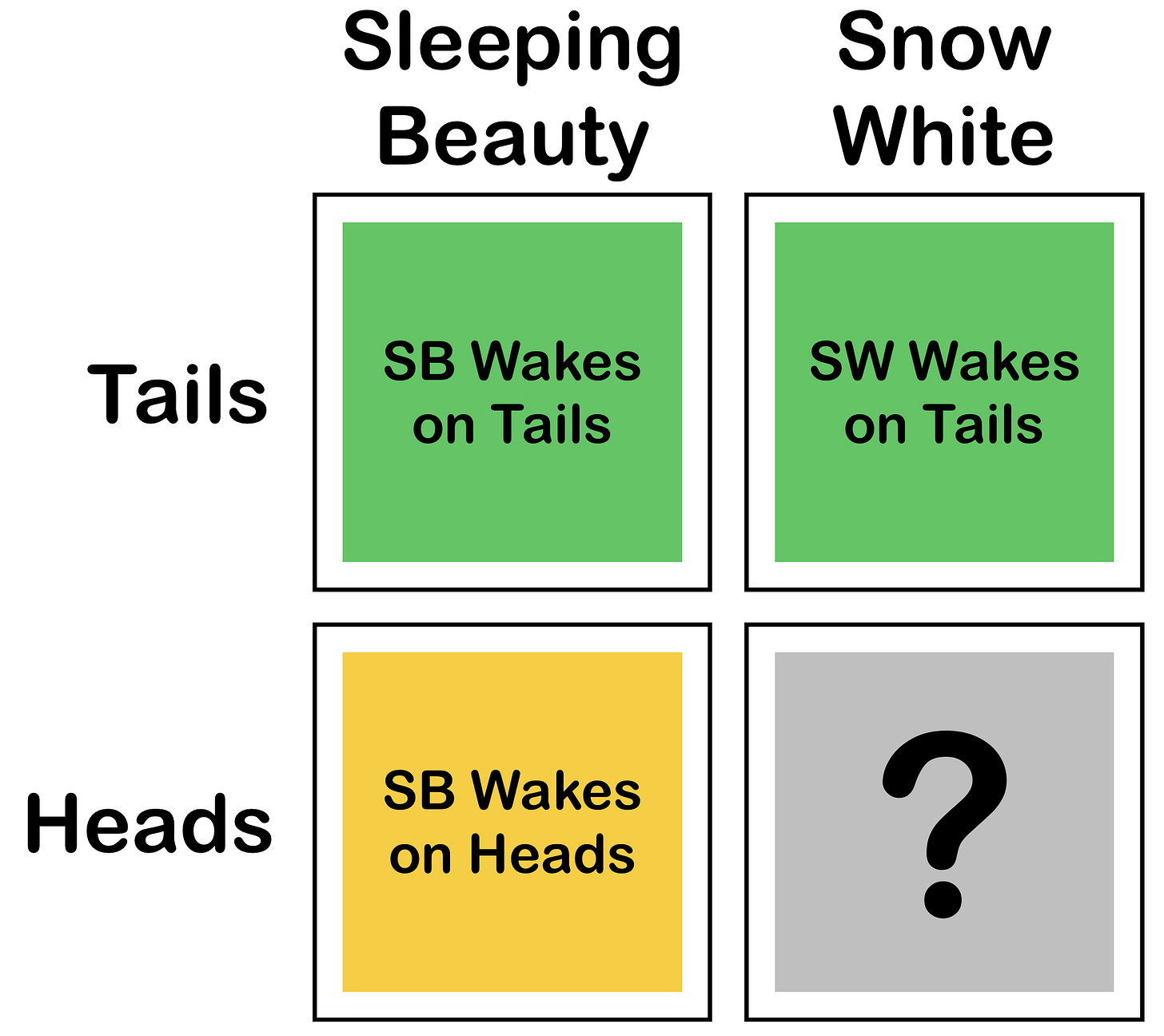
What’s actually happened is that we’ve broken down the game into four separate scenarios, like so:
Each square of this picture corresponds to a possible outcome of the game. For instance, there are three squares where someone wakes up. Since one of them is heads, the odds of heads are 1/3. The 50% chance of not waking on heads refers to the case in the lower right - the scenario where Snow White stays asleep.
This actually isn’t odd - it’s a completely correct solution to the way we’ve phrased the problem. Where things get weird is when you try to apply these learnings to the universe question.
For instance, suppose we’re trying to figure out whether we live in universe A with 50 billion people or universe B with 100 billion. If it turned out we were actually in universe A, then under this interpretation we would still need to account for the other 50 billion people - they couldn’t just be discarded, they had to exist in both universes in order for the math to work.
In an old lecture on this topic, Scott Aaronson referred to this interpretation as a “warehouse of souls.2 Basically, this version of the SIA requires us to posit that all possible people who might exist actually do - just not necessarily in this or any other actual universe.
I suppose one might be tempted to take a theistic approach here and say these are just souls in heaven (or some equivalent) waiting to be incarnated. But aside from being unconvincing to anyone who didn’t already believe in that sort of thing, it would be a misunderstanding of the situation.
The truth is that even “warehouse of souls” is a misnomer. It’s the closest English phrase to what the theory is suggesting, but it’s wildly underselling it. The warehouse interpretation is saying that first, before the universe is even created, before we even consider or bring into the equation whatever entity is responsible for it, there are already a bunch of people, possibly infinite. This is actually super problematic for a theistic perspective: in this model “God” would be one of those things that would have to come after all the people exist. In order for the warehouse interpretation to prove God, you must be willing to concede that the souls of all these people would have existed even if God never did. All God did was put them in a universe!
This is not some obscure technical point. These “souls” weren’t something I introduced arbitrarily: they were an unavoidable iron-clad consequence of our particular mathematical statement that “the odds of waking on tails are twice that of heads.” And that means they aren’t just hypothetical - if we take this interpretation of the SIA, we have to account for its real world consequences3
This is also why I introduced Snow White at the start of this section. Because without her, with only Sleeping Beauty, it was completely impossible to make this concept cogent. What would a “missing” second wake up on heads correlate to in the real world? “Warehouse of souls” doesn’t make sense without a second person - it would just be Sleeping Beauty’s soul twice.
But in introducing Snow White, we actually did change what we were saying slightly. Notice that Snow White existed before we even started this game - P(A | H) was only set to 50% because tails left Snow White still sleeping. Suppose instead that neither Snow White or Sleeping Beauty existed at all until the coin was flipped, at which point one or both of them were created directly as a consequence of the flip. In this case P(A | H) goes back to 100%, because Snow White literally doesn’t exist when the coin lands heads - there is only 1 person and therefore 100% of all people are awake. That would put us right back to the SSA and P(H | A) = 1/2.
That’s because the SSA models the situation as follows: “First, select a cause for the universe (God, bing bang, etc.) Then, use that to fill the universe with people.”
The “warehouse” interpretation, on the other hand, models the situation as “first select a bunch of people, then select a universe to place them in.” That interpretation might make sense for the Snow White version of the Sleeping Beauty Problem, but definitely doesn’t work as a model of creation.
Interpretation 2: Betting
I would suspect that many proponents of the SIA don’t really love the implications of the “warehouse of souls” interpretation. And I agree that it seems a bit unnecessary to keep around all those unused souls. Can we do better?
One way is to formalize the statement “you should bet on the universe that has the most observers.” To do that, for each universe we would take the probability of that universe (50% for heads or tails) and multiple by the number of people in that universe, then select the maximum. In math:
We’re now making our decision based on something that isn’t literally a probability. If it were, it would need to be either P(H | A) or P(A | H), which would put us back into the warehouse interpretation. Instead, we’ve just come up with a completely different thing, and we’re using that to make a decision.
This is a completely normal thing to do. Many will recognize H* as essentially the expectation value function. Expected values, not probabilities, are typically what we use to make decisions anyway, so there’s some merit in it.
So let’s change the game again, this time adding a reward. Before the game starts, the scientists open a bank account for SB. Every time she wakes up and guesses what the coin said, she gets $100 for making the correct guess, and when the experiment is over she can keep any money she earns.
Obviously, we can all agree that in this scenario she should always bet “tails.”
Unfortunately, our goal isn’t to guess correctly the most times, it’s to properly calibrate our odds of being correct. Those aren’t the same things - there is in fact a fundamental differences between bets and probabilities.
Here’s an illustration: suppose I came to you with an offer to flip a coin, letting you choose heads or tails. If you choose heads and win, I’ll give you a dollar. If you choose tails and win, I’ll give you two dollars.
In this case only a moron would choose heads - you might as well, you have absolutely nothing to lose. But, just as obviously, that doesn’t actually mean tails is more likely! The odds would still be 50-50.
I could make this even more obvious. Suppose I offer to charge you $100, and in exchange I’ll flip a coin 20 times. If it comes up heads every single time (roughly one-in-a-million), I’ll give you a billion dollars. If you were using “expected return” as your metric for betting, then this bet would be a no-brainer. And in some cases, you could argue that taking this bet would still be totally rational - maybe $100 is so little to you that you don’t mind almost certainly losing it for a one-in-a-million shot.
What would never ever be rational, however, would be taking this bet and expecting to actually win, especially if this game were only played once.45
I hope the connection here is clear. Of course, the Sleeping Beauty problem isn’t really about earning anything, and in the original SB problem instead of maximizing reward this approach would maximize “number of people who make the correct decision.” The important point here is that probability and expectation are two different concepts, and for both the original SB problem and especially the universe question, the probabilities are the things we care about.
Just as you don’t get paid unless the coin actually comes up heads 20 times, people who don’t exist don’t get to make guesses about reality. If God’s existence really does mean there are an infinite number of people, and regular physics “only” predicts a trillion, then if God were unlikely there would probably only be a trillion people. It doesn’t matter how many people would have been correct for believing in God if he existed, because he doesn’t. If we all used expectation to make our guess, we would all be wrong.
The Problem of Infinity
Infinities, by the way, are a huge problem for the SIA, because they break our formula for expectation. If a universe X has infinite size, then (size of X) * P(X) = ∞, even if P(X) is really really small6
To hammer this home, we’re going to push the SB game to the absolute limit7 The scientists will flip 100 trillion coins, and if every single one comes up tails, they will wake Sleeping Beauty up an infinite number of times. If even one coin comes up heads, just a single one, they will wake her up once.
The odds of infinite wake ups would have approximately 30 trillion zeros. And yet, the SIA would tell us that we must assume that that is what happened, because no positive number is so small that you can multiple it by infinity without getting infinity. In fact, our formula says that we would have to assign literally zero probability to the event that scientists got anything other than 100 trillion tails8
This gets even worse when you consider different kind of infinities, like Beth numbers. For those who don’t know, there isn’t actually one amount which we call “infinity.” Rather, infinities are in a hierarchy, where for any infinity, you can always create a bigger one. The smallest infinity is the number of integers, followed by the number of real numbers, and the hierarchy goes up from there, with each level infinity larger than the level below it. The Beth numbers mark each level of this hierarchy: Beth-0 is the integers, Beth-1 is the real numbers, etc.
And because each Beth number is infinitely larger than those below it, once you start using them in the SIA, the math becomes utterly unsalvageable. It stops mattering how unlikely an event is, merely having Beth-N people is enough to obliterate the odds of any lower Beth number. I could literally propose the most absurd thing I can think of, something like “we are all just sentient hallucinating blueberries in a muffin with Beth-987 people” and as long as the odds of that weren’t literally zero (which they might not be, right? I mean, sure, the odds are roughly 1 in a gazillion zillion, but they aren’t literally zero) then it would automatically be infinitely more likely than any theory that had Beth-986 people or fewer, which includes, for instance, the Beth-2 God in Bentham’s Bulldog’s argument for theism.
“Ah!” you might say, “but the muffin is obviously absurd. Almost any other Beth-987 explanation would be better. A Beth-987 God would be astronomically more likely, for instance.”
This is true. But in return I could simply propose a Beth-988 muffin, and that is not just astronomically more likely than your Beth-987 God, it’s literally in all senses of the word infinitely more likely. And this game would continue on and on forever without end.
That’s the real problem here. It’s not just that we’re forced to draw an absurd conclusion - it’s that there’s always going to be a larger muffin, and because of this we are unable to draw literally any conclusion about anything. A single culinary absurdity has made any understanding of our universe mathematically impossible.
Interpretation 3: Urns
The last interpretation of the SIA is one I thought I had read on Wikipedia, but can no longer find and therefore am unable to properly attribute (sorry). I’m including it not because I think anyone actually uses it, but because I think it nicely illustrates why the SSA works and the SIA doesn’t.
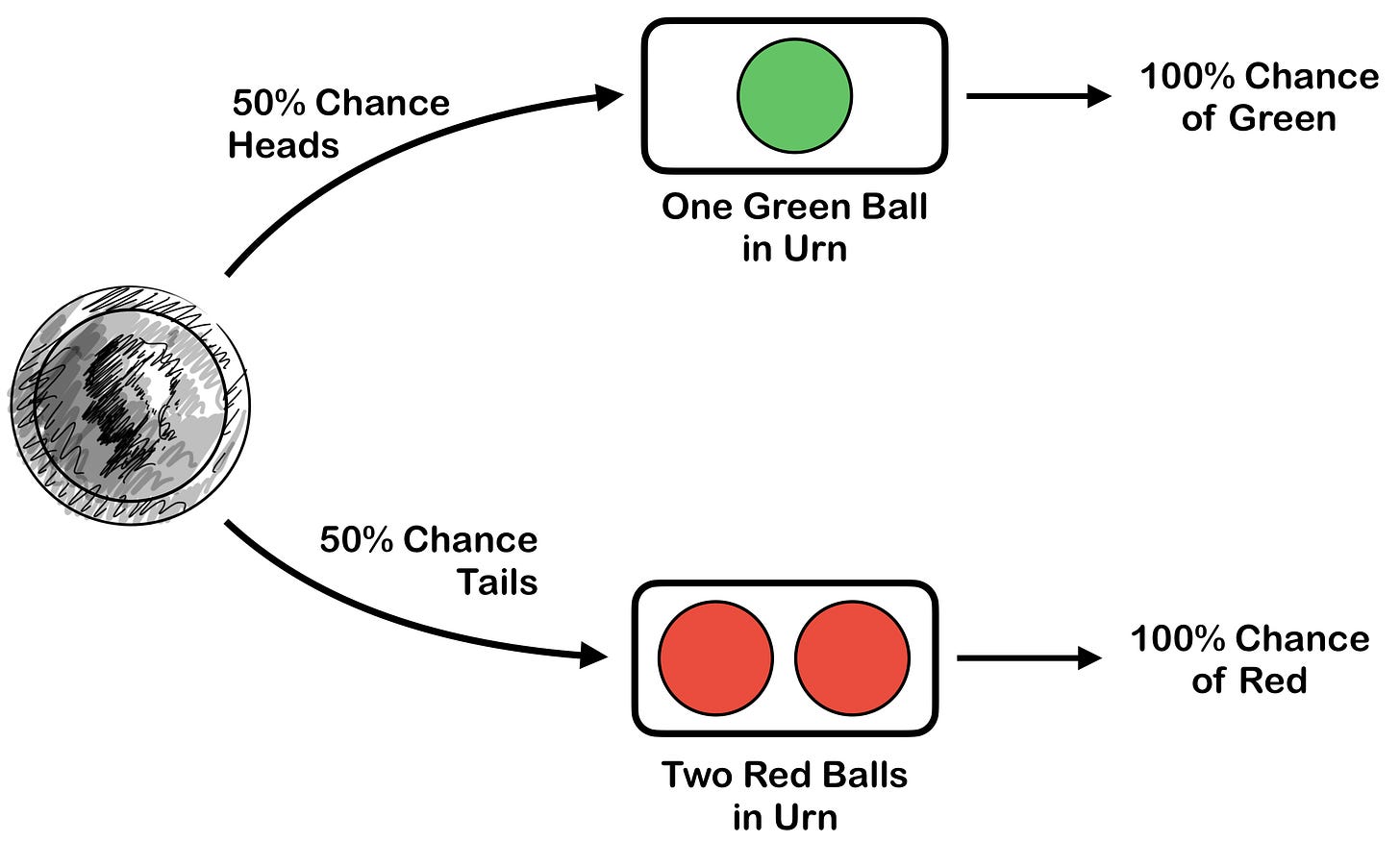
It’s essentially this: suppose we flip a coin. On heads we place a green ball in an urn, and on tails we place two red balls in an urn. We do this some super large number of times, until the urn is basically full. Then we pull out a ball. The argument is that the SSA corresponds to “what are the odds we put a green ball into the urn on the next flip?” and the SIA corresponds to “what are the odds we take out a green ball from the urn?”
The first thing I’ll say is that I disagree the Sleeping Beauty problem corresponds to either of those scenarios, and the reason I disagree is that in the SB problem the coin isn’t being flipped over and over again - it’s being flipped once. This matters, because if you flip the coin only once then the odds of pulling a green ball or a red ball (what is supposed to be the “SIA” event) are actually exactly the same - 50% each. Here’s a handy illustration:
Only one color ever goes in after each coin flip, so only one color can ever go out. The only deciding factor is whether the coin was heads or tails.
I think some SIA supporters are implicitly assuming that some law of large numbers will kick in and average out the probabilities, but it doesn’t. To have that happen, you would need to flip the coin and over and again, creating lots and lots of observers, some in “Universe H,” some in “Universe T.” Eventually, once you’ve done this enough, you would find that all of the original information about the coin - whether it had been heads or tails - would be lost. Then, and only then, would your odds of finding yourself in a “heads universe” finally be 1/3.
If we tried to use this as a model for understanding our universe, we would be assuming that all possible universes exist - a universe with God, a universe without, the Forever Muffin, whatever else you can think of. That’s even worse than the warehouse interpretation which only assumed all people exist.9
I’ll end by returning to a statement I made very early on, about all observers not being equally likely. Take a closer look at the urn flow chart above and imagine that, on the two red balls, we wrote a number one and a number two. What are the odds of getting any particular ball? For green, it’s still 50%, but for red, it’s 25% for ball #1 and 25% for ball #2. That’s why SB works out to the halfer position, because even though there are twice as many observers on tails, you are half as likely to be either one.
Bonus Interpretation: Just Fudge It
This one’s not really an interpretation, but I wanted to cover the case where we say “screw interpretations, let’s just force the math to work!” In other words, could we just say P(H | A) = 1/3 and P(A) = 1 and just leave it at that?
Unsurprisingly, this doesn’t work. Since P(A) and P(A | H) will both be 1, you wind up with:
Meaning your coin itself has 1/3 chance of coming up heads, which is clearly wrong. This is kind of obvious in retrospect, since we’re just doing the math of the SSA using different inputs.
What about other interpretations?
I’d like to think I’ve covered 99% of the arguments thirders tend to make. But obviously, I can’t be sure of that. There may be other interpretations, but even if there are, even if there are literally hundreds of interpretations I’ve missed, I don’t think it matters.
Math is math, and at the end of the day the SB problem is just a math problem. There’s only one to properly define the question we want to ask, and when we define it that way, there’s only one answer we’ll ever get. Any attempt to get a different answer while asking the same question - any slight modification or fancy argument that seems to yield differing results - must either be asking something else or saying something incorrect. The fact of the matter is that the laws of mathematics are not so easily swayed. The most we could possibly be doing is fooling ourselves.
And the truth is unfortunately quite unsatisfying. The SSA essentially tells us that the fact of our existence provides no evidence to change our understanding of the universe. It’s a shame to be sure, but I think that honestly, we should have been able to predict this from the very start. The SIA, in its effort to conjure infinite people through mere reasoning alone, is nothing more than a philosophical shortcut. It’s expecting to get something for free. But mere logic simply isn’t strong enough to for that, and it never will be.
We’re not going to worry about the fact that we can’t define a measure over different universes, because virtually all of our logic would apply for any possible measure you could conceive of. When it doesn’t, it should be taken to mean a measure over our prior intuitions. This will be different for everyone but as long as everyone is willing to give some arbitrarily small amount of support to any proposal we are fine.
I’m not sure if he first coined that term, but I couldn’t find it elsewhere through googling.
There are other weird consequences to this approach. For instance, nothing in this interpretation tells you how large the warehouse should be. P(A | T) must be twice P(A | H), but either one can be as high or low as we want. We assumed there were only two people, but the math would be identical if there were a million or even an infinite number of people, so long as none of them actually woke up, i.e. they ”stayed in the warehouse”.
Since I suspect someone will point this out, this is not about the diminishing value of money as you acquire more of it. If it were, then the arguments here would not apply to the Sleeping Beauty problem. Rather, it is simply a much more banal illustration that probabilities are not the same things as expectations. And, in this particular case, we are trying to be correct about probabilities, we don’t care about the expectation.
For an interesting example of why expectation is not always a rational approach to betting, see The St. Petersburg Paradox. Although the St. Petersburg Paradox is a bit like using a sledgehammer to hit a nail - you can see how expectation fails much easier with the examples I give.
Some of you may point out that the SSA has issues with infinity too, since you cannot select uniformly over an infinite set over observers. True, but it is possible to use our finite intuition to define a version of the SSA to circumvent this: simply define P(U | A) = P(U) when U is an infinite universe. With SIA, you can patch some holes but at the end of the day the number of observers is appearing directly in your equations and that means the issues I discuss below are unfixable.
Inspired by Bentham’s Bulldog’s published paper.
Nick Bostrom made a similar argument to the one presented here in what he called the “Presumptuous Philosopher.” I obviously agree with his logic, but if I had to make one critique, it would be that his phrasing (choosing “a trillion” people over a “a trillion trillion”) isn’t nearly visceral enough. People are notoriously bad at visualizing large numbers, and it’s way too easy to miss the weightiness of this issue. I prefer the Forever Muffin.
This, by the way, is a lot worse than Tegmark’s Mathematical Universe Hypothesis. That only assumed all mathematical objects existed. This assumes the existence of any random crap I could make up on the spot, including the Forever Muffin.







Thanks for writing this! Some of it resembles my stance on the topic, particularly around "expect like a thirder, believe like a halfer." (https://utopiandreams.substack.com/p/anthropic-reasoning)
I'm curious if you encountered/read Joe Carlsmith's essays arguing for SIA > SSA.
https://joecarlsmith.com/2021/09/30/sia-ssa-part-1-learning-from-the-fact-that-you-exist
He presents a bunch of arguments that SSA leads to insane conclusions there that I don't see you engaging with. (I can be more specific if that would be helpful.)
gah wrote a long comment but substack deleted it when i accidentally swiped off.
I'm a thirder who believes in SIA, but I acknowledge that I have no idea what to do when infinity gets involved. I used to be a double halfer like you seem to be, but I was convinced over. Obviously I disagree that P(A)=P(A | H)=1, because A should be "this very awakening occurs", which will lead to the standard P(H | this awakening) Bayes equation that I'm sure you've seen thirders use before in their papers.
The interesting thing with Sleeping Beauty problem is that indeed anthropic reasoning is very odd and strange, and it has wide implications. I'll give one of the standard thirder vibes-based interpretation instead of getting too bogged down in the Bayes:
If heads, woken up once. If tails, woken up a million times in a row, mind erased each time, of course.
I can vividly imagine waking up, unsure of the day, and being asked whether I think the coin came up heads, and thinking of the potential thousands, tens of thousands, hundreds of thousands of people with my same conscious experience that came before or will come after me that were asked the same question. I consider what they felt -- were they unsure? Groggy? tired? did one of them see a butterfly? did a hundred of them see the same bug in the corner of the room that I see? And I think thinking of them each as individual perspectives with individual, unique experiences is best. If I’m just one “observer-moment” plucked out of that huge sea of near-duplicates, the mere fact that I find myself awake at all is way better explained by the scenario that provided a million of these unique experiences than a scenario which provides a single one.